Convexified Modularity Maximization for Community Detection
In many modern systems, e.g., recommender systems, similar objects form hidden clusters and we are interested in recovering the clusters based on observation of pairwise interactions among the objects. The data of pairwise interactions can be represented as a graph consisting of nodes representing objects and edge connections encoding pairwise interactions. Community detection aims to find the clusters, i.e., the dense subgraphs, in a large graph.
We propose a new methodology for community detection. It is based on a semidefinite programming relaxation
of the classical (generalized) modularity maximization formulation, followed by a doubly weighted L1-norm k-median
clustering:
Step 1. Solve the SDP program below with $\lambda=1/\sum_{i=1}^n d_i$ for $\widehat{Y}$
Step 2. Solve the doubly weighted k-median problem below with $ k = r$, and output the resulting $ r $-partition of $[n]$
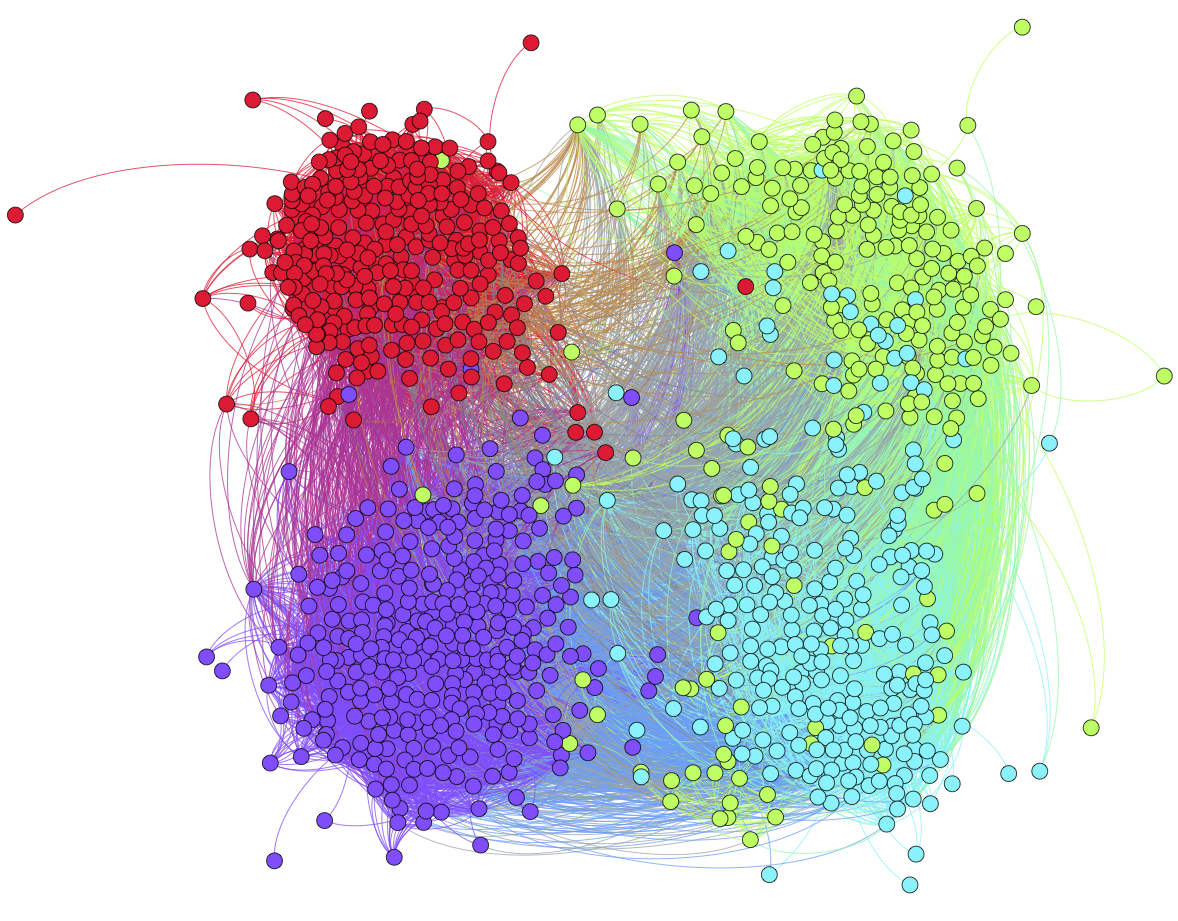
On the left, we show a facebook friendship network formed by students at Simmons College. Nodes are colored according to the clustering result of convexified modularity maximization. The 4 clusters are found to be correlated with the graduation years.
Semidefinite programming (SDP)
Let $A$ denote the adjacency matrix of graph $G$, and $d$ denote the vector of node degrees.
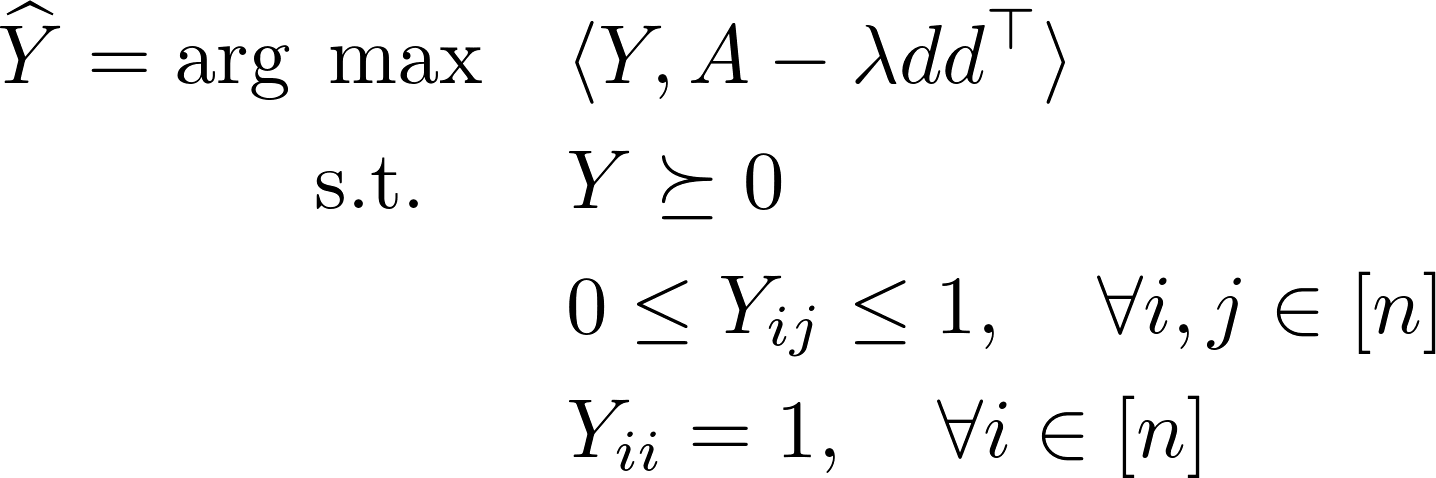
Here $\langle B, C \rangle={\rm Trace} (B^\top C)$ denotes the
usual scalar product by treating matrices as vectors,
and we write $B \succeq 0$ if $B$ is positive semidefinite.
Solving SDP by generic methods can be quite slow.
Here we use the alternating direction method of multipliers (ADMM) to solve the SDP.
Let $\max\{ X, Y \}$ be the matrix whose $(i,j)$-th entry is given by $\max\{X_{ij}, Y_{ij}\}$;
the matrix $ \min\{ \mtx{X}, \mtx{Y} \}$ is similarly defined.
For a symmetric matrix $X$ with an eigenvalue decomposition $X= U \Sigma U^\top$,
let $( X )_{+} := {U} \max \{ \Sigma, 0 \} U^\top$,
and let $(X )_{I}$ be the matrix obtained by setting all the diagonal entries of $X$ to $1$.
Let $J$ denotes the $n \times n$ all-one matrix.
The ADMM algorithm for solving the SDP with the dual update step size equal to $1$, is given as follows:
1. Initialization: $ Z^{(0)} = \Lambda^{(0)} = 0$, $ k=0 $ and $\texttt{MaxIter} =100$.
2. while $k < \texttt{MaxIter}$
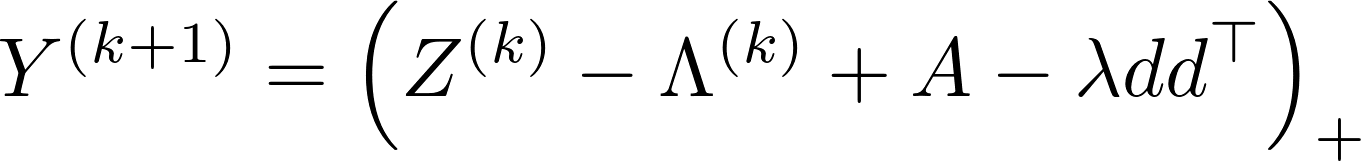
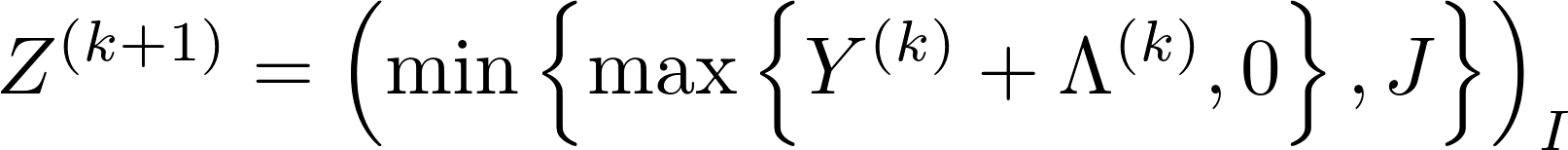
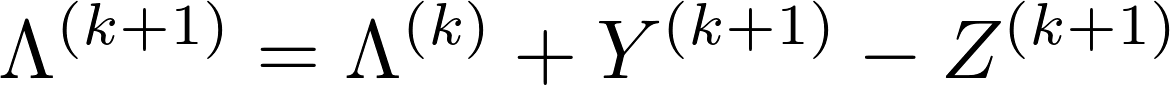
end while
3. Output the final solution
Doubly weighted k-median clustering
The $i$-th row of $\widehat{Y}$ can be viewed as a feature vector for node $i$, and one can cluster nodes by clustering the corresponding rows of $\widehat{Y}$. Here we multiply the columns of $\widehat{Y}$ by the corresponding degrees to obtain $\widehat{W}=\widehat{Y} {\rm diag}(d)$. The $i$-th row of $\widehat{W}$ can be viewed as a weighted feature vector. Next we cluster the row vectors of $\widehat{W}$ using a weighted k-median clustering. In particular, we solve the following program for a partition $C_1,...,C_r$ of $[n]$ and $r$ cluster centers $x_1,...,x_r \in \mathbb{R}^n$:
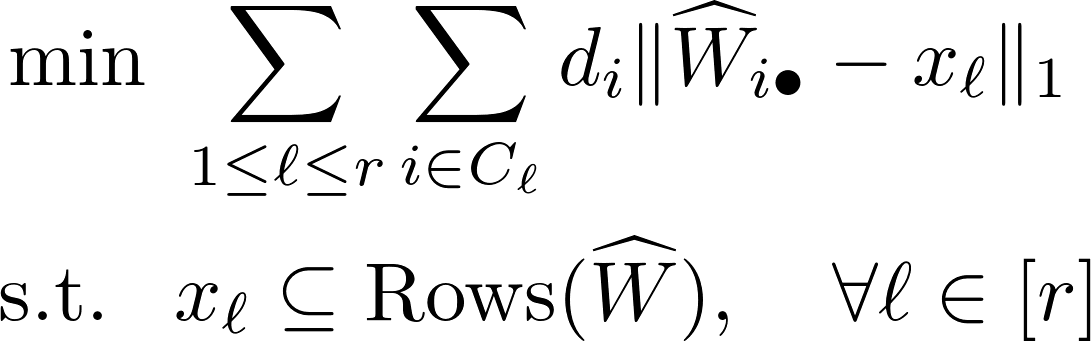
Code
We provide the matlab source code for our algorithmPaper
Yudong Chen, Xiaodong Li, and Jiaming XuConvexified modularity maximization for degree-corrected stochastic block models
arXiv:1512.08425. Dec. 2015.