Block Form Representations of Integer/Linear Optimization Problems
with Relational Databases
by
Peter L. Jackson and James Rappold
April 1996
School of Operations Research and Industrial Engineering
Cornell University, Ithaca NY 14853
LPSQL is a software system for formulating integer/linear optimization problems using a block form representation of the optimization program and a Structured Query Language (SQL) representation of the data. The block form representation is a simple, compact, and convenient modelling approach that lends itself to SQL extension. The SQL approach permits software engineers to easily extend existing database applications to support optimization applications.
A prototype version of LPSQL including model database, model editor, and matrix generator has been written by Peter Jackson and James Rappold using Microsoft Access and Visual Basic Professional for the Microsoft Windows (3.1) operating system. The current version of the matrix generator is designed to call Sunset Software XA to solve the resulting integer/linear programs.
These prototypes are intended for non-profit research and educational purposes. Copies of the prototypes under development may be obtained from the World Wide Web using "http://www.orie.cornell.edu/~jackson". No warranties are expressed or implied concerning these prototypes. The source code for these prototypes is the intellectual property of the authors. The authors reserve the right to commercialize later versions of these products.
There are many commercial packages on the market for managing optimization projects but, to our knowledge, none of them has adopted the particular approach taken in LPSQL. The most similar package is MATHPRO by David Hirshfeld. MATHPRO pioneered the block form representation but it is currently limited to a proprietary database approach. We have adopted most of the conventions for block form representations from MATHPRO.
In the practical application of linear optimization, it becomes important to make a clear separation between the linear optimization model, the data used to drive the model, and the linear programming solver code used to solve the model. The purpose of this separation is to permit specialization of the functions associated with the project.
There are three important types of specialization in an optimization project. Consider an application of linear programming to production planning and scheduling. There are three functions that may be associated with different individuals in the project: the planner, the management analyst, and the software engineer.
The production planner is responsible for committing the company to a course of action that entails commitments to customer deliveries, machine time allocation, work force levels, minimum inventories, and supplier orders, among others. The planner looks to software applications for assistance in formulating production schedules and to cope with the volume of transactions needed to execute those schedules. The planner is a software user. He or she is responsible for maintaining the integrity, and currency of the production planning database, for executing the optimization solver whenever the data have changed, for interpreting the results of the model solution, and for modifying suggested schedules to account for situations or factors not considered by the optimization model. Specialization occurs because, in many cases, it is not necessary, or practical, for the planner to have more than a rudimentary understanding of formal optimization concepts.
When the planner is not trained in formulating optimization models, it is necessary for a management analyst to develop such models. The analyst must formulate a generic family of models that will provide good schedules for the planner on a routine basis. The analyst must be capable of a high degree of abstraction: translating the requirements of the planner into the formal construct of an optimization model and, from there, translating these constructs into a detailed specification of the data requirements of the model.
The software engineer is responsible for designing a database system and for creating integrating software that will provide an intuitive interface for the planner to maintain the database, and to analyze and execute production schedules.
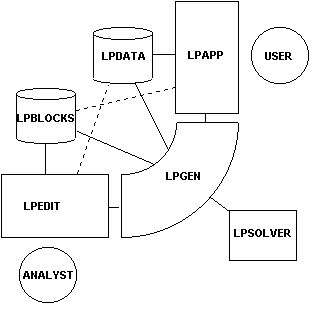
From the perspective of a software engineer, the diagram below suggests a conceptual organization to the software involved in a linear programming project.

LPBLOCKS: a relational database containing the optimization model descriptions and the SQL statements that link the model to the data in LPDATA.
LPDATA: a relational database containing the data of the model.
LPEDIT: software for editing the model descriptions stored in LPBLOCKS.
LPAPP: the interface software designed for the user. Among its many functions, it must permit the user to maintain and edit the data stored in LPDATA, and to view and modify the solution from optimization programs. This program would be custom written by the software engineer for the particular application.
USER: the individual responsible for the LPDATA database, interacting with LPAPP.
ANALYST: the individual responsible for the LPBLOCKS database, interacting with LPEDIT.
LPGEN: software for generating the optimization model based on a particular model description in LPBLOCKS and using current data from LPDATA, and for writing the solution back into LPDATA. LPGEN can be called from LPEDIT and from LPAPP.
LPSOLVER: software for solving a linear optimization model.
A prototype database for LPBLOCKS has been designed by Peter L. Jackson. It describes integer/linear optimization problems using a block form representation. All relationships between LPBLOCKS and LPDATA are expressed as SQL queries which are written by the analyst. In this way, no restrictions have been imposed on the design of the LPDATA database, apart from the limitations inherent in the SQL approach.
A prototype for LPEDIT has been written by Peter L. Jackson. It features a point-and-click tabular interface for editing block form representations of integer/linear optimization problems, a mouse-driven dialog box for creating SQL queries, and a pivot-style tabular view of individual matrices.
A prototype for LPGEN has been written by James Rappold. It reads the model description from the LPBLOCKS database and uses the SQL queries found there to extract all the model data from LPDATA. To solve the resulting MILP, it calls the dynamic link library XADLL.DLL which may be obtained separately from Sunset Software.
Version 1 prototypes assume that the databases are implemented in Microsoft Access format.
In the following sections, we describe three different statements of a simple production planning problem.
English Statement of the Production Planning Problem
Algebraic Statement of the Production Planning Problem
Block Statement of the Production Planning Problem
Choose values for the production quantity and inventory of each product in each time period so as to minimize the total cost of production and holding inventory subject to the constraints that (1) for each product and each time period, the production of that product less the increase in inventory of that product is equal to the demand for that product in that time period (net of initial inventory), (2) for each workcenter and each time period, the total number of hours required to produce the products planned for production in that time period does not exceed the total number of hours of production available in that workcenter in that time period, and (3) production and inventory may not be negative for any product in any time period.
Also, impute the value (or cost, if negative) of an additional unit of demand for each product in each time period and impute the value of an additional hour of production time available for each workcenter in each time period.



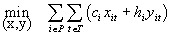
subject to:
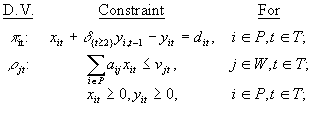
where
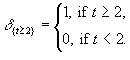
Product in Products: indexes a particular product, Product, in the set of all products, Products.
Workcenter in Workcenters: indexes a particular workcenter, WorkCenter, in the set of all workcenters, Workcenters.
Time in TimePeriods: indexes a particular time period, Time, in the set of all time periods, TimePeriods.
PRODCOST(Product): cost of producing one unit of product, Product, Product in Products.
HOLDCOST(Product): cost of holding one unit of product, Product, in inventory for one time period, Product in Products.
DEMAND(Product,Time): forecast demand, in units, for product Product in time period Time net of initial inventory, Product in Products, Time in TimePeriods.
CAPACITY(WorkCenter,Time): number of hours of production available in workcenter WorkCenter and time period Time, WorkCenter in WorkCenters, Time in TimePeriods.
IOMATRIX(Product,WorkCenter): number of production hours required in workcenter WorkCenter per unit of production of product Product, Product in Products, WorkCenter in WorkCenters.
PROD(Product,Time): number of units of production of product Product in time period Time, Product in Products, Time in TimePeriods.
INV(Product,Time): number of units of inventory of product Product at the end of time period Time, Product in Products, Time in TimePeriods.
DEM(Product,Time): implied value per unit of product Product in time period Time, Product in Products, Time in TimePeriods.
CAP(WorkCenter,Time): implied value per hour of production in workcenter WorkCenter in time period Time, WorkCenter in WorkCenters, Time in TimePeriods.
MIN LHS PROD INV RHS OBJ PRODCOST HOLDCOST DEM DEMAND 1 -1/+1(Time) DEMAND CAP IOMATRIX CAPACITY LOB 0 0 UPB
Table of Contents
The labels LHS, RHS, OBJ, LOB, and UPB are reserved names standing for "left hand side," "right hand side," "objective," "lower bound," and "upper bound," respectively. The shaded cells in the table lie at the intersection of these class names and are never used. The remaining cells can be used to construct a specific problem statement. The block problem statement is a tabular way of writing the following linear program, expressed using matrix notation:
Minimize OBJ = (PRODCOST) * PROD + (HOLDCOST) * INV
Subject to
DEMAND<= (1) * PROD + (-1/+1(Time))*INV <=DEMAND
- (IOMATRIX) * PROD <=CAPACITY
0<= PROD <+INFINITY
0<= INV< +INFINITY
where parentheses are used to indicate matrices of "appropriate dimension." Dimensions are discussed in the section "Interpreting Dimensions."
Observe that a blank cell in the LHS column or in the LOB row is interpreted as -. A blank cell in the RHS column or in the UPB row is interpreted as +. A blank cell anywhere else is interpreted as 0. Since the matrix DEMAND occurs in both the LHS and RHS columns, we could rewrite the first row as:
(1) * PROD + (-1/+1(Time))*INV = DEMAND.
The dimension of any matrix or vector in the matrix problem statement can be deduced from the block format and from the variable definitions.
The dimension of a row or column is defined to be the dimension of the variable class named by the row or column. Thus, the dimension of the column labelled PROD is the dimension of the PROD variable class, namely |Products| * |TimePeriods|, where |Set| means the number of elements in Set. Similarly, the dimension of the row labelled CAP is |WorkCenters|*|TimePeriods|. The dimension of columns LHS and RHS and of rows OBJ, LOB, and UPB are each taken to be 1.
Column labels are taken to be row vectors and row labels are taken to be column vectors. Thus, PROD and INV are taken to be vectors of primal variables with dimension 1 x |Products| * |TimePeriods|. Similarly, DEM is a vector of dual variables with dimension |Products| * |TimePeriods| x 1, and CAP is a vector of dual variables with dimension |WorkCenters|* |TimePeriods| x 1.
For any cell in the table, the dimension of the block (matrix) implied by that cell is the product of the row dimension and the column dimension. For example, the cell at the intersection of row CAP and column PROD must have dimension equal to dimension |WorkCenters| *|TimePeriods| x |Products|*|TimePeriods|. The matrix referred to by the cell is IOMATRIX which was defined to have dimension |WorkCenters| x |Products|. Note that there is a mismatch between the defined dimension of IOMATRIX and the implied dimension. For this reason, we have enclosed the symbol IOMATRIX in parentheses. Special rules are required to determine how to expand IOMATRIX into a block of the appropriate dimension. These rules will be discussed below.
The literals "1" and "-1/+1(Time)" are enclosed in parentheses. These symbols represent matrices of appropriate dimension and special rules are required to determine the construction of these matrices from the underlying data.
The power of the block form representation comes from the natural way in which matrices which are defined with small dimension can be expanded into blocks (larger matrices) of much larger dimension. To illustrate, consider the block represented by (IOMATRIX). As mentioned, the implied dimension of this block is |WorkCenters| *|TimePeriods| x |Products|*|TimePeriods|. The defined dimension of IOMATRIX is |WorkCenters| x |Products|.
We first assume that the indices of the matrix are members of the union of row indices and column indices. It would be an error, therefore, if IOMATRIX were defined with indices RawMaterial and Product, where "RawMaterial in RawMaterials" is defined as another index. This is an error because the neither the row CAP nor the column PROD uses index RawMaterial.
Now, consider a generic element of the block (IOMATRIX). It would have two column index values: product and columntime. It would have two row index values: workcenter and rowtime. From the matrix IOMATRIX, we can retreive a value based on product and workcenter: call it IOMATRIX(product,workcenter). We set the element of the block equal to this value only if the time index values match; that is, only if rowtime=columntime. Otherwise, the element of the block is zero. To summarize:
(IOMATRIX)(workcenter,rowtime,product,columntime)
= IOMATRIX(product,workcenter), if rowtime= columntime;
= 0, otherwise.
To take another example, consider the literal "1" at the intersection of the DEM row and the PROD column. The dimension of the block (1) is |Products| * |TimePeriods| x |Products| * |TimePeriods|. A generic entry in this block has column index values: columnproduct and columntime. The entry has row index values: rowproduct and rowtime. The literal has 0 dimension. The rule for determining the value of the entry is:
(1)(rowproduct,rowtime,columnproduct,columntime)
= 1, if rowproduct=columnproduct, and rowtime=columntime;
= 0, otherwise.
That is, since the column indices match with the row indices, (1) must represent the identity matrix. Thus, the matrix product (1)*PROD = PROD.
Suppose we replaced the matrix IOMATRIX in the block form with a literal "1". What would a generic entry of this block be? The implied dimension of the block doesn't change. It is still |WorkCenters| *|TimePeriods| x |Products|*|TimePeriods|. A generic entry would be given by
(IOMATRIX)(workcenter,rowtime,product,columntime)
= 1, if rowtime= columntime;
= 0, otherwise.
That is, for every combination of product and workcenter there would be a "1" in this block if the time index from the column matches the time index from the row. In this case, the matrix product (1)*PROD represents a vector of, for each workcenter, the sum all production quantities across all products. So the interpretation of a literal depends critically on how the column indices match the row indices.
Suppose there are six indices: a in A, b in B, c in C, d in D, e in E, and f in F. Let ROW represent a row variable class with indices a, c, e, and f. Let COL represent a column variable class with indices b, c, d, and f. Let M represent a matrix with indices a, b, and c. Suppose we write M at the intersection of the COL column and the ROW row in the block form:
b,c,d,f
MIN LHS COL RHS
OBJ
a,c,e,f ROW M
LOB
UPB
Observe that this situation includes the possibility that the matrix is defined in terms of an index that appears in the row class but not the column class (i.e., a), an index that appears in the column class but not the row class (i.e., b), and an index that appears in both row and column classes (i.e., c). Of indices not mentioned in the matrix definition, this situation includes a row class index that is not shared by the column class (i.e., e), a column class index that is not shared by the row class (i.e., d), and an index that is shared by both the row class and the column class (i.e., f).
The implied dimension of the block at the intersection of COL and ROW is |A|*|C|*|E|*|F| x |B|*|C|*|D|*|F|. A particular column of the COL variable class would have index values b, cc, d, fc. A particular row of the ROW variable class would have index values a, cr, e, fr. The subscripts are used to distinguish between the row and column index values. The value of the block entry at the intersection of this particular row and column is given by the following general rule:
(M)(a,cr,e,fr,b,cc,d,fc)
= M(a,b,c), if fr=fc, and cr=cc=c ;
= 0, otherwise.
Special cases of the general rule can be deduced by omitting indices. For example, suppose we omit the existence of indices c in C and f in F. Then, we have
(M)(a,e,b,d)
= M(a,b).
As another example, suppose we omit indices a in A, and b in B, and define the matrix M to have a single index, c in C. Then,
(M)(cr,e,fr,cc,d,fc)
= M(c), if fr=fc, and cr=cc=c ;
= 0, otherwise.
As a final example, suppose we omit indices a in A, b in B, and c in C. Then, logically, the matrix M has zero dimension. It would have to be replaced by a number. Let the number be denoted m. Then,
(M)(e,fr,d,fc)
= m, if fr=fc ;
= 0, otherwise.
To apply the rule for blocks in the borders of the block form (OBJ, LHS, RHS, LOB, and UPB), note that each of these blocks has a row or column dimension equal to one. For this dimension, imagine it has an index: one in ONE, where |ONE|=1. The rule is easily applied to these situations.
Certain matrices occur frequently in linear optimization models so it makes sense to define special functions that will generate these matrices automatically. We have currently defined only one such function but later versions of LPSQL may include more. The literal "-1/+1(Time)" in the production planning example actually represents a function defined on the set TimePeriods x TimePeriods as follows:
"-1/+1(Time)"(rowtime,columntime)
= -1, if rowtime = columntime -1;
= +1, if rowtime = columntime;
= 0, otherwise.
In the Production Planning Example, the block represented by the cell at the intersection of INV and DEM is denoted (-1/+1(Time)). From the indices of the row and column classes, we deduce that this block has dimension |Products| * |TimePeriods| x |Products| * |TimePeriods|. Applying the definition of the "-1/+1(Time)" function with the general rule for expanding matrices, we have that a generic entry in this block has the following value:
(-1/+1(Time))(rowproduct,rowtime,columnproduct,columntime)
= -1, if if rowproduct=columnproduct and rowtime = columntime -1;
= +1, if rowproduct=columnproduct and rowtime = columntime;
= 0, otherwise.
Thus, the coefficients of the inventory variables in the material balance equations are easily represented by the "-1/+1(Time)" literal.
The Structured Query Language is a standard way of describing queries into relational databases. The basic SQL query is of the form "SELECT fieldnames FROM table WHERE criteria ORDER BY fieldname(s)" where table names a particular data table in the database, criteria indicates which records to retrieve from the table, fieldnames indicates a list of fields of the records to retrieve and fieldname(s) indicates which fields to sort the resulting recordset by. The result of a query is a recordset: a series of records, each record with the same fixed set of data fields.
The data of an integer/linear optimization problem are the contents of the index sets and the contents of the matrices. In the LPSQL system, these data are assumed to reside in a single database known to the system as LPDATA. The model resides in the database known as LPBLOCKS. The links between the model and the data are stored as data definitions in LPBLOCKS. Each index set and each matrix in the model must have associated with it an SQL query as part of its definition. The definition must indicate which field in the resulting dataset yields the value being sought. In addition, for matrices, the definition must indicate which fields in the resulting dataset match the indices defined for the matrix.
For example, the index set Products may have associated with it an SQL statement of the form "SELECT ProductId FROM ProductTable". It would also specify "ProductId" as the field of the recordset to use to obtain the elements of the set Products.
The matrix PRODCOST may have associated with it an SQL statement of the form "SELECT ProductId, UnitCost FROM ProductTable". It would specify "UnitCost" as the field of the recordset to use to obtain the elements of the matrix PRODCOST. The matrix PRODCOST is defined to have an index "Product in Products". The definition must indicate which field in the recordset will match the index Product. In this case, the definition would match the field ProductId with the index Product.
Hirshfeld, David S. MathPro. MathPro, Inc. P.O. Box 3404, West Bethesda, Maryland 20827-0404